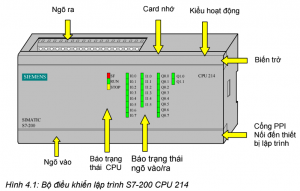
Tự động hóa
PLC S7 200_Bài 8: Thiết kế theo logic Bool & biểu đồ Karnaugh
8. Thiết kế theo logic Bool & biểu đồ Karnaugh
8.1 Giới thiệu
Quá trình chuyển đổi một mục tiêu điều khiển thành một chương trình theo ngôn ngữ LAD, FBD hay STL yêu cầu phải thông qua một cấu trúc. Đại số BOOL là một trong các công cụ cần thiết để phân tích và thiết kế những hệ thống này.
8.2 Đại số BOOL
Đại số BOOL được phát triển vào năm 1800 bởi một nhà toán học người Ai-len tên là James Bool. Nó cực kỳ hữu ích trong thiết kế các mạch số. Nó vẫn được sử dụng nhiều bởi các kỹ sư điện và tin học. Phương pháp thực hiện là mô hình hệ thống logic bằng các công thức riêng lẻ. Công thức có thể là sự kết hợp của các AND/OR đơn giản thành các dạng mới. Với cùng phương pháp này, người thiết kế mạch có thể ứng dụng cho lập trình ở LAD.
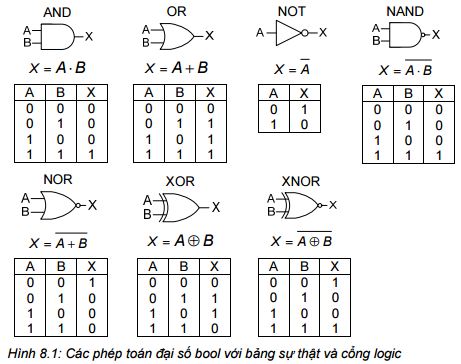
Công thức Boolean bao gồm nhiều biến và các hoạt động giống như các công thức đại số thông thường. Ba phép toán cơ bản là AND, OR và NOT, hoặc tổ hợp của các phép toán cơ bản là NAND, NOR, XOR, XNOR. Các phép toán với bảng sự thật được cho ở hình 4.1. Mỗi phép toán được trình bày bởi một công thức đơn giản với hai biến được sử dụng là A và B để tính giá trị X. Bảng sự thật là một phương pháp đơn giản để mô tả tất cả các tổ hợp có thể có là cho ngõ ra ở trạng thái “ON” hoặc “OFF” (“1” hoặc “0”).
Chú ý: Cổng XOR thường được chuyển thành các cổng tương đương như sau:
Chú ý: Khi đơn giản các biểu thức đại số Bool, phép tóan OR có ưu tiên thấp nên chúng được thực hiện trước. Phép toán NOT có ưu tiên cao nhất, nên chúng được đơn giản sau. Cách thức thực hiện có thể minh họa cho việc đơn giản một biểu thức đại số như sau:
8.3 Thiết kế Logic
Các ý tưởng thiết kế có thể được chuyển đổi trực tiếp từ các biểu thức đại số Bool, hoặc bằng các phương pháp khác (ở các chương sau). Các biểu thức đại số Bool có thể được đơn giản hoặc sắp xếp lại và sau đó chuyển sang sơ đồ LAD hoặc FBD hay ở ngôn ngữ STL.
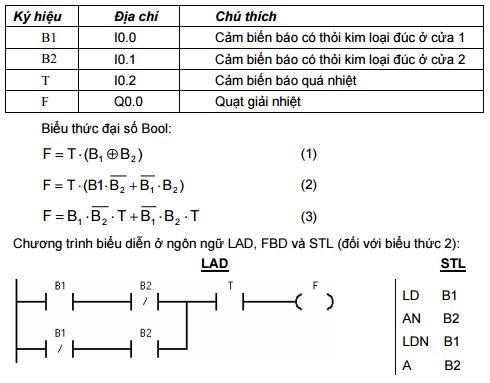
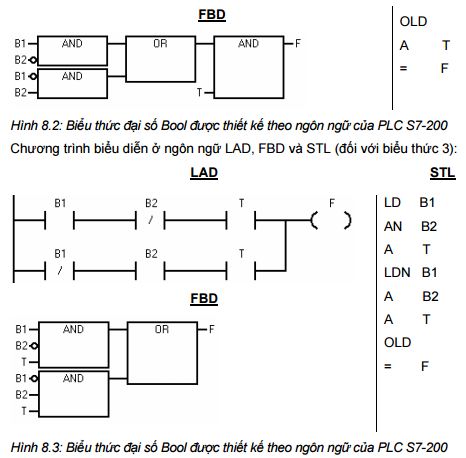
Nếu chúng ta mô tả một qui trình điều khiển bằng lời, thì chúng ta thường có thể chuyển trực tiêp nó thành biểu thức đại số Bool như ở hình 8.2 và hình 8.3. Trong ví dụ, việc mô tả quá trình được đưa ra trước. Trong các ứng dụng thực tế, điều này có được nhờ vào các bộ phận cơ của hệ thống. Trong nhiều trường hợp hệ thống chưa có, việc thực hiện sẽ là một bài tóan cho người thiết kế. Bước kế tiếp là xác định bộ điều khiển nên làm việc như thế nào. Trong trường hợp này, các câu lệnh được viết ra trước tiên, và sau đó chuyển đổi thành biểu thức đại số Bool. Biểu thức đại số Bool có thể được chuyển đổi theo dạng mong muốn. Công thức đầu tiên chứa một XOR, nó không thể biểu diễn dược ở dạng LAD, như vậy nên chuyển nó thành dạng các cổng tương đương sử dụng AND, OR và NOT.
Ví dụ 8.1: Điều khiển nhiệt độ lò nhiệt
Mô tả quá trình:
Một lò nhiệt có hai cửa có thể cấp nhiệt cho thỏi kim loại đúc ở mỗi cửa. Bộ phát nhiệt cung cấp đủ nhiệt cho hai thỏi kim loại đúc. Nhưng nếu chỉ có một thỏi kim lọai đúc thì nhiệt độ cung cấp trở nên quá nóng, để giảm nhiệt độ thì một quạt giải nhiệt cho lò sẽ được bật.
Mô tả điều khiển:
Nếu nhiệt độ quá cao và chỉ có một thỏi kim loại đúc ở một cửa thì bật quạt.
Giải
Bảng xác định input/output:
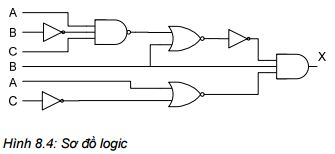
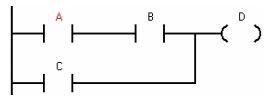
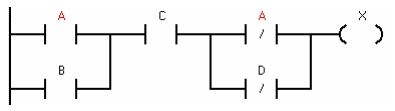
Ví dụ 8.2: Hãy chuyển sơ đồ logic sau đây (hình 8.4) thành chương trình trong PLC ở ngôn ngữ LAD, FBD và STL:
Giải:
![]()
![]()
![]() Nếu cứ giữ nguyên sơ đồ logic thì việc chuyển đổi chương trình ở LAD sẽ gặp nhiều khó khăn vì trong PLC không thể biểu diễn được cổng NAND và NOR. Vì vậy để đơn giản hơn, ta sử dụng phương pháp biến đổi sơ đồ thành biểu thức đại số Bool và sau đó đơn giản biểu thức này.
Nếu cứ giữ nguyên sơ đồ logic thì việc chuyển đổi chương trình ở LAD sẽ gặp nhiều khó khăn vì trong PLC không thể biểu diễn được cổng NAND và NOR. Vì vậy để đơn giản hơn, ta sử dụng phương pháp biến đổi sơ đồ thành biểu thức đại số Bool và sau đó đơn giản biểu thức này.
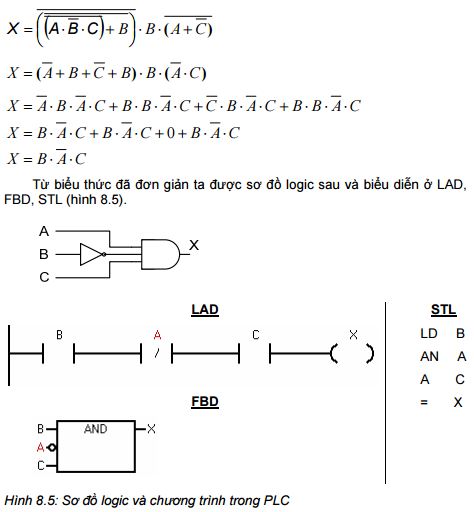
Sơ đồ trên được biểu diễn ở dạng biểu thức đại số Bool và sau đó được đơn giản.
Tóm lại, ta sẽ thu được các biểu thức đại số Bool từ việc mô tả yêu cầu công nghệ hoặc một sơ đồ mạch hoặc một sơ đồ LAD. Các biểu thức có thể được đơn giản bằng cách sử dụng các định lý của đại số Bool. Và sau đó từ biểu thức này ta có thể chuyển thành ngôn ngữ LAD, FBD hay STL trong PLC. Khi đơn giản các biểu thức đại số Bool ta cần chú ý một số quy tắc cơ bản sau:
- Loại bỏ các cổng NOT không cần thiết. Thông thường có thể thực hiện bằng cách thay thế các cổng NAND và NOR bằng một biểu thức đơn giản hơn sử dụng định lý DeMorgan.
- Lọai bỏ các công thức phức tạp như XOR.
Các qui tắc này có thể được mô tả như ví dụ sau:
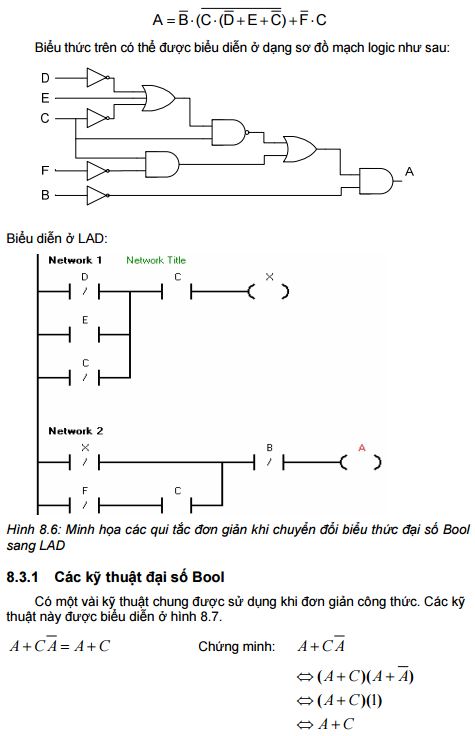
Ví dụ 8.3: Cho biểu thức điều khiển:
8.4 Các dạng logic chung
Khi biết một tập các dạng logic đơn giản sẽ cung cấp cho người thiết kế giải quyết các chiến lược điều khiển. Các dạng sau được cung cấp để sử dụng trực tiếp hoặc ý tưởng khi thiết kế.
8.4.1 Dạng cổng phức
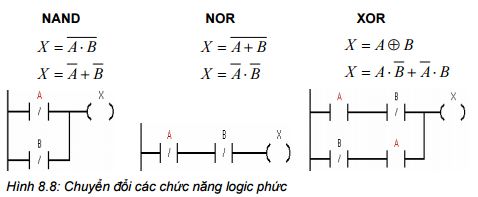
Tổng cộng có 16 loại cổng logic khác nhau có 2 ngõ vào. Dạng đơn giản nhất là AND và OR, các cổng khác là các cổng phức. Ba cổng phức thông dụng được thảo luận trước đây là NAND, NOR và XOR. Các cổng này có thể được biểu diễn thành dạng đơn giản hơn chỉ với các cổng AND và OR tương ứng ở sơ đồ LAD trong PLC biểu diễn ở hình 8.8.
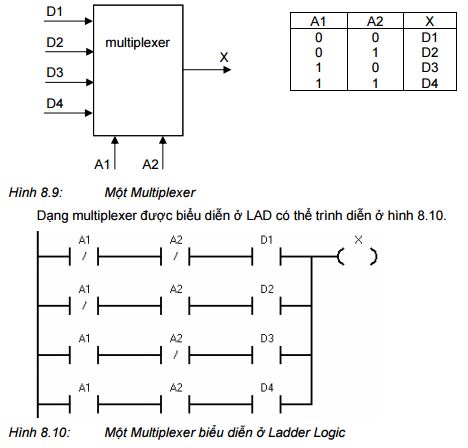
8.4.2 Multiplexers
Multiplexers là sự đa hợp các thiết bị được kết nối với một thiết bị đơn. Nó rất thông dụng trong các hệ thống điện thoại. Một chuyển mạch điện thoại được sử dụng để xác định điện thoại nào sẽ được kết nối.
Hình 8.9 là một bộ multiplexer. Ngõ ra X sẽ được kết nối với một trong 4 ngõ vào D1, D2, D3 hoặc D4 tùy thuộc vào giá trị của các ngõ A1 và A2.
8.5 Một số ví dụ thiết kế đơn giản với đại số bool
Các trường hợp sau đây minh họa các vấn đề logic tổ hợp khác nhau và các giải pháp có thể thực hiện. Hãy đọc kỹ mô tả trước khi xem lời giải.
8.5.1 Các chức năng logic cơ bản
Yêu cầu 1: Viết một chương trình sao cho ngõ ra D ở mức logic “1” khi công tắc A và B đóng lại hoặc khi công tắc C được đóng.
Giải quyết:
D = (A × B) + C
Hình 8.11: Chương trình được viết ở LAD
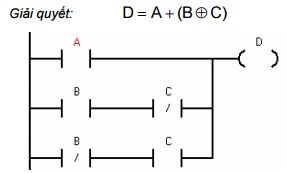
Yêu cầu 2: Viết một chương trình sao cho ngõ ra D ở mức logic “1” khi nút ấn A được ấn, hoặc chỉ B hoặc chỉ C được ấn.
Giải quyết:
Hình 8.12: Chương trình được viết ở LAD
8.5.2 Hệ thống an toàn xe hơi
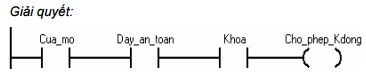
Yêu cầu: Viết chương trình ở LAD cho một hệ thống an toàn cửa xe hơi/dây an toàn chỗ ngồi. Khi cửa mở, hoặc dây an toàn chưa được thắt thì việc khoá khởi động không thể thực hiện được. Nếu tất cả được thực hiện thì khóa có thể khởi động được động cơ.
Hình 8.13: Chương trình hệ thống an toàn xe viết ở LAD
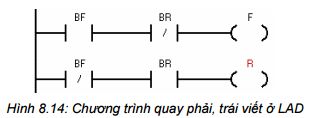
8.5.3 Quay phải/trái động cơ
Yêu cầu: thiết kế một bộ điều khiển động cơ có một nút nhấn quay phải và một nút nhấn quay trái. Các ngõ ra quay phải và trái sẽ chỉ ở “1” khi một trong các nút nhấn được ấn. Khi cả hai nút nhấn được ấn thì động cơ không làm việc.
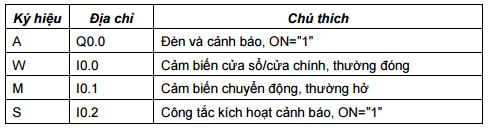
8.5.4 Cảnh báo trộm
Cảnh báo trộm cho một ngôi nhà như sau: khi có sự xâm nhập của kẻ trộm thì cảnh báo và đèn báo được kích hoạt. Cảnh báo này được kích hoạt nếu kẻ xâm nhập bị phát hiện bằng cảm biến gắn ở cửa sổ và một bộ phát hiện chuyển động. Cảm biến ở cửa sổ là loại thường đóng, khi cửa sổ vỡ do kẻ trộm xâm nhập thì cảm biến bị ngắt. Cảm biến nhận biết chuyển động được thiết kế để khi một người được phát hiện thì ngõ ra sẽ ở mức “1”. Ngoài ra còn có một công tắc để kích hoạt/không kích hoạt cảnh báo. Hoạt động cơ bản của hệ thống cảnh báo, các ngõ vào và ra của bộ điều khiển được cho ở bảng sau:
Hoạt động cơ bản của cảnh báo có thể được mô tả theo qui tắc:
- Nếu cảnh báo là “ON”, kiểm tra cảm biến.
- Nếu cảm biến cửa sổ/cửa chính bị ngắt, bật âm thanh cảnh báo và đèn báo sáng.
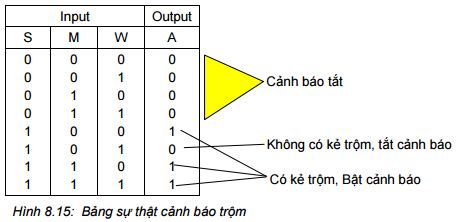
Bước kế tiếp là xác định công thức điều khiển. Trong trường hợp này có 3 ngõ vào khác nhau và 1 ngõ ra, bảng sự thật được trình bày ở hình 8.15.
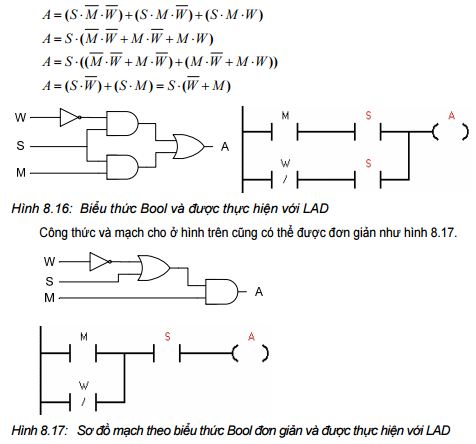
Biểu thức Boolean và đơn giản được cho ở hình 8.17 được viết từ bảng sự thật hình 8.16.
8.6 Biểu đồ Karnaugh
8.6.1 Giới thiệu
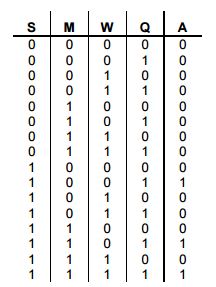
Bảng Karnaugh cho phép chúng ta chuyển đổi một bảng sự thật thành biểu thức Boolean đơn giản mà không sử dụng đại số Bool. Trong mục 8.5.4 của chương này có một ví dụ về cảnh báo trộm. Hình 8.18 là bảng sự thật của nó với một ngõ vào báo yên tĩnh được thêm vào.
Đã cho: A, W, M, S như trước đây, tức là:
Và:
Q = Báo yên tĩnh (0 = yên tĩnh)
Bước 1: Vẽ bảng sự thật
Bảng sự thật của mạch cảnh báo trộm nhưhình 8.18. Thay vì chuyển đổi trực tiếp bảng này thành biểu thức, thì ta đặt vào một bảng được chỉ ở hình 8.19. Dòng và cột được chọn từ các biến ngõ vào.
Việc quyết định các biến nào sử dụng cho các dòng hoặc các cột có thể tùy ý và các bảng sẽ trông khác nhau nhưng vẫn sẽ cho một kết quả giống nhau. Đối với các biến ở cả hai dòng và cột thì được sắp xếp theo thứ tự chỉ giá trị của bit sử dụng NOT. Trình tự không phải là nhị phân, nhưng được tổ chức để chỉ có một bit thay đổi tại một thời điểm. Như vậy trình tự của bit là 00, 01, 11, 10. Bước này rất quan trọng. Kế tiếp là đưa các giá trị là “1” trong bảng sự thật vào bảng Karnaugh. Giá trị “0” cũng có thể được đưa vào nhưng không cần thiết.
Hình 8.18: Bảng sự thật mạch cảnh báo trộm
Trong ví dụ, ba giá trị “1” từ bảng sự thật được đưa vào trong bảng.
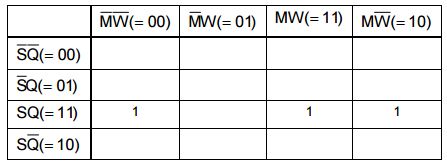
Bước 2: Chia các biến vào.
Ở đây chọn SQ và MW
Bước 3: Vẽ bảng Karnaugh dựa vào các biến vào
Hình 8.19: Bảng Karnaugh
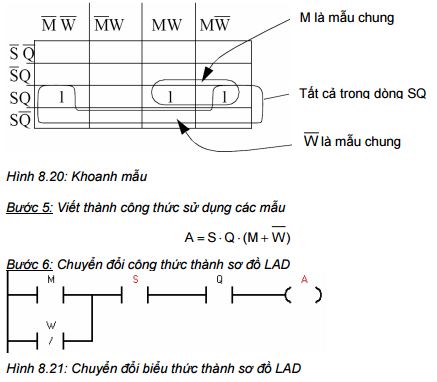
Khi các bit được nhập vào bảng Karnaugh sẽ có một vài mẫu rõ ràng. Các mẫu tiêu biểu này có phần nào đối xứng. Hình 8.20 có hai mẫu được khoanh tròn. Trong trường hợp này, một mẫu có hai bit đứng kề nhau. Mẫu thứ hai thì khó nhìn thấy hơn vì các bit nằm ở bìa bên phải và trái của cột.
Sau đó các mẫu có thể được chuyển thành biểu thức Boolean. Để thực hiện trước tiên ta quan sát các mẫu đặt ở dòng thứ ba cho nên biểu thức sẽ được AND với SQ. Kế tiếp là tìm bit chung trong hai mẫu. Ta thấy trong mẫumột có M chung, mẫu 2 có W chung. Những cái này bây giờ có thể tổ hợp thành công thức. Cuối cùng công thức được chuyển thành sơ đồ LAD.
Bước 4: Tìm kiếm mẫu trong bảng
Bảng Karnaugh là một phương pháp có thể được chọn để đơn giản biểu thức thay cho đại số Bool. Nó giúp cho người học dễ dàng hơn trong việc đơn giản các biểu thức. Ở ví dụ trên chỉ có 4 biến, như vậy chỉ có hai biến ở dòng và hai biến ở cột. Nếu có nhiều biến hơn vẫn có thể sử dụng. Ví dụ nếu có năm biến ngõ vào thì ta có thể sử dụng ba biến cho dòng hoặc cho cột với các mẫu là 000, 001, 011, 010, 110, 111, 101, 100. Nếu có nhiều hơn một ngõ ra, thì ta tạo bảng Karnaugh cho mỗi ngõ ra.
8.7 Câu hỏi và bài tập
BT 8.1: Cổng logic được biểu diễn ở ngôn ngữ LAD cho ở dưới đây là cổng AND hay OR?
BT 8.2: Vẽ một sơ đồ hình thang với ngõ ra D là “1” khi công tắc A và công tắc B được đóng hoặc khi công tắc C được đóng.
BT 8.3: Vẽ một sơ đồ hình thang với ngõ ra D là “1” khi nút nhấn A được ấn hoặc B hoặc C được ấn.
BT 8.4:
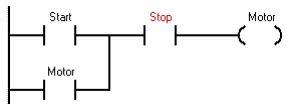
- Giải thích tại sao nút nhấn stop phải là thường đóng và nút nhấn start phải là thường hở.
- Xem xét một trường hợp một ngõ vào PLC được nối với nút nhấn thường đóng làm nút nhấn stop. Tiếp điểm được sử dụng trong ngôn ngữ LAD là thường hở như được cho ở dưới. Tại sao cả hai là không giống nhau? (ví dụ cùng là NC hoặc NO)
BT 8.5:. Tạo một chương trình đơn giản ở ngôn ngữ LAD theo bảng sự thật được cho ở dưới với ngõ ra ở trạng thái “ON” khi các nút nhấn tương ứng được ấn.
- Đơn giản biểu thức.
- Viết thành chương trình ở ngôn ngữ LAD theo biểu thức đã đơn giản.
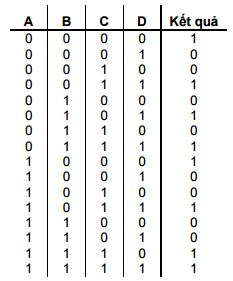
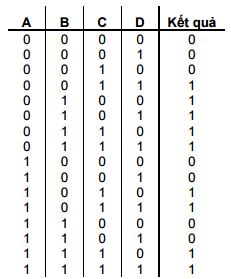
BT 8.13: Cho bảng sự thật sau
- Chỉ ra tổ hợp nào cho kết quả là 1.
- Viết kết quả ở a) thành biểu thức đại số Bool.
- Đơn giản biểu thức Bool ở b)
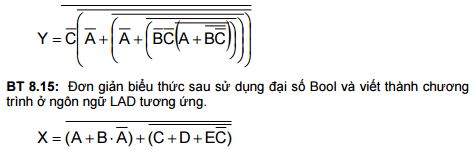
BT 8.14: Đơn giản biểu thức sau thành đơn giản nhất và viết thành chương trình ở ngôn ngữ LAD.
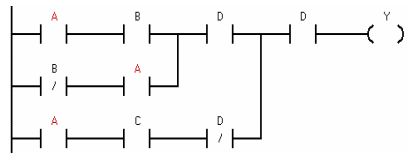
BT 8.16: Chuyển đổi chương trình biểu diễn ở LAD sau thành biểu thức đại số. Sau đó đơn giản nó và chuyển lại ở ngôn ngữ LAD.
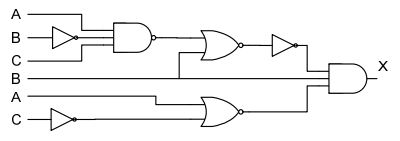
BT 8.17: Cho sơ đồ mạch logic như hình vẽ
- Viết thành biểu thức ở mạch logic đã cho.
- Đơn giản biểu thức này.
- Vẽ lại sơ đồ mạch đơn giản hơn theo câu b).
![]()
![]() BT 8.18: Cho một hệ thống được mô tả theo biểu thức sau:
BT 8.18: Cho một hệ thống được mô tả theo biểu thức sau:
- Đơn giản biểu thức sử dụng đại số Bool.
- Thực hiện sơ đồ mạch số theo biểu thức ban đầu và biểu thức đã được đơn giản ở câu a).
- Viết thành chương trình ở ngôn ngữ LAD theo biểu thức ban đầu và biểu thức đã được đơn giản ở câu a)
BT 8.19: Đơn giản biểu thức đã cho và sau đó viết thành chương trình ở ngôn ngữ LAD và sơ đồ mạch số theo biểu thức ban đầu và biểu thức đã đơn giản.
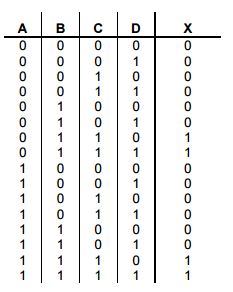
BT 8.20: Lập bảng Karnaugh theo bảng sự thật dưới đây.
BT 8.21: Sử dụng bảng Karnaugh để đơn giản bảng sự thật sau và viết thành chương trình ở ngôn ngữ LAD.
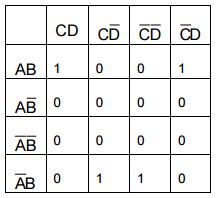
BT 8.22: Viết ra biểu thức đơn giản nhất đối với bảng Karnaugh được cho dưới đây
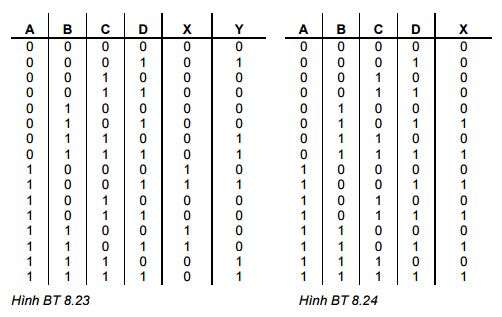
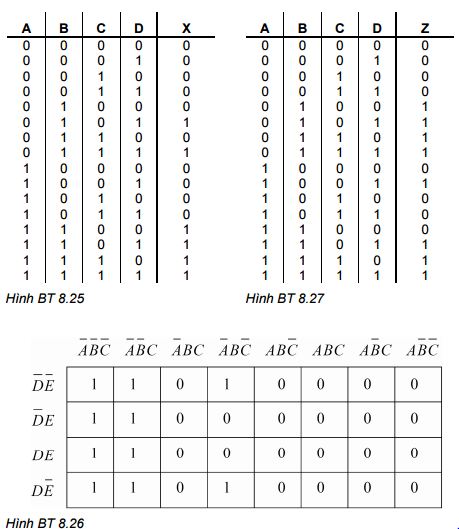
BT 8.23: Cho bảng sự thật ở hình BT 8.23 và viết thành chương trình PLC ở ngôn ngữ LAD với sự trợ giúp bằng kỹ thuật đơn giản biểu thức là bảng Karnaugh hay đại số Bool.
BT 8.24: Kiểm tra bảng sự thật ở hình BT 8.24 và viết thành chương trình PLC ở ngôn ngữ LAD sử dụng bảng Karnaugh.
BT 8.26: Cho bảng sự thật ở hình BT 8.25 với các ngõ vào A, B, C và D và ngõ ra X. Chuyển nó thành chương trình PLC ở LAD sử dụng bảng Karnaugh.
BT 8.25: Tìm biểu thức Boolean đơn giản nhất đối với bảng Karnaugh được cho ở hình BT 8.26 mà không sử dụng đại số Bool. Viết chương trình ở LAD.
Hình BT 8.26
BT 8.27: Cho bảng sự thật như hình BT 8.27
- Tìm biểu thức đại số Bool sử dụng bảng Karnaugh.
- Vẽ sơ đồ LAD sử dụng bảng sự thật (không phải biểu thức Boolean).
BT 8.28: Chuyển đổi sơ đồ LAD sau thành bảng Karnaugh.
BT 8.29:
- Xây dựng bảng sự thật cho các vấn đề sau đây:
- Có 3 nút nhấn A, B, C.
- Ngõ ra là “1” nếu bất kỳ hai nút nhấn nào được ấn.
- Nếu C được ấn thì ngõ ra sẽ luôn luôn “1”.
- Viết thành biểu thức Bool.
- Viết thành biểu thức Boolean sử dụng bảng Karnaugh.
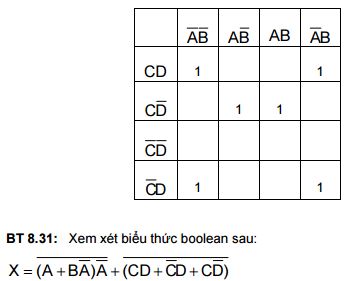
BT 8.30: Viết ra biểu thức Boolean đơn giản nhất đối với bảng Karnaugh dưới đây
- Bằng đồ thị.
- Bằng đại số Boolean.
- Biểu thức Boolean này có thể được chuyển trực tiếp thành LAD. Giải thích nếu cần thiết, thực hiện bất kỳ các thay đổi được yêu cầu để có thể chuyển thành LAD.
- Viết ra ở LAD, dựa vào kết quả ở bước a).
- Đơn giản biểu thức sử dụng đại số Bool và viết ra LAD mới.
- Viết bảng Karnaugh đối với biểu thức Boolean, và cho biết nó có thể được sử dụng để thu được biểu thức Bool đơn giản như thế nào.